
Ch4-1. 트리
코딩 인터뷰 완전 분석(저 : 게일 라크만 맥도웰) 참조
이진 트리
이진 트리는 각 노드가 최대 두 개의 자식 노드를 갖는 트리를 말한다.
자식 노드가 세개인 경우는 삼진 트리라고 부른다.
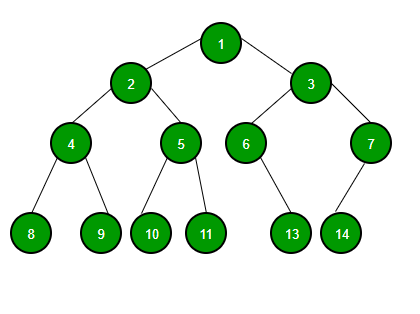
아래와 같은 트리는 최대 자식 노드가 두개이므로 이진 트리이다.
이진 탐색 트리
이진 탐색 트리는 모든 노드가 다음과 같은 순서를 따르는 이진 트리를 뜻한다.
“모든 왼쪽 자식 노드 <= n < 모든 오른쪽 자식 노드” 조건이 모든 노드 n에 대해서 반드시 참인 경우 이진 탐색 트리이다.
조건은 바로 아래 자식 노드뿐 아니라 모든 자식 노드에 대해서 참이어야 한다.

위와 같은 경우, 모든 노드가 조건을 만족하므로 이진 탐색 트리이다.
예를 들어, 13은 8과 10보다는 크지만 14보다는 작으며 4는 8과 6보다는 작지만 3보다는 크다.
트리의 종류
완전 이진 트리(complete binary tree)
완전 이진 트리란 트리의 마지막 단계(Level)을 제외한 모든 높이에서 노드가 꽉 차 있어야 한다.
마지막 단계는 꽉 차 있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야 한다.

위의 그림은 완전 이진 트리가 맞지만 만약 L 노드가 F 노드의 right child 였다면 완전 이진 트리가 아니다.
전 이진 트리(full binary tree)
전 이진 트리는 모든 노드가 자식이 없거나 정확히 두 개 있는 경우이다.
다시 말해, 자식이 하나만 있는 노드가 존재해서는 안된다.
포화 이진 트리(perfect binary tree)
포화 이진 트리는 완전 이진 트리이면서 전 이진 트리인 경우이다.
모든 말단 노드가 같은 높이에 있고, 말단 노드의 개수가 최대이다.

포화 이진 트리의 노드 개수는 2k+1-1 개 이다. (k는 트리의 height)
이진 트리 순회
중위 순회(in-order traversal)
중위 순회는 왼쪽 가지, 현재 노드, 오른쪽 가지 순서로 노드를 방문하고 출력하는 방법이다.
이진 탐색 트리를 중위 순회한다면 오름차순으로 방문하게 된다.
전위 순회(pre-order traversal)
전위 순회는 자식 노드보다 현재 노드를 먼저 방문하는 방법이다.
전위 순회에서는 루트 노드를 가장 먼저 방문하게 된다.
후위 순회(post-order traversal)
후위 순회는 모든 자식 노드를 먼저 방문하고 마지막에 현재 노드를 방문하는 방법이다.
후위 순회에서는 루트 노드를 가장 마지막에 방문하게 된다.
이진 힙
힙은 최댓값 및 최솟값을 빠르게 찾아내기 위해 고안된 완전 이진 트리이다.
부모노드의 키값이 자식노드의 키값보다 항상 작은 힙을 “최소 힙” 이라 하며, 그 반대는 “최대 힙”이라 한다.
키값의 관계는 부모와 자식 노드 사이의 관계만 성립하며, 형제 사이에 대소관계는 성립하지 않는다.
삽입 연산
최소힙에 원소를 삽입할 때, 가장 밑바닥 오른쪽 위치로 삽입한다.(완전 트리의 속성에 위배되지 않기 위해서)
그 다음 삽입된 원소가 알맞은 자리를 찾을 때까지 부모 노드와 교환해 나간다. 이와 같은 방식으로 최소 원소를 위쪽으로 올린다.
이 연산은 힙에 있는 원소의 개수를 n개라 할 때, O(long n) 시간이 걸린다.
최소 원소 뽑아내기
최소힙에서 최소 원소는 언제나 가장 위에 위치한다.
최소 원소를 제거한 후, 힙에 있는 가장 마지막 원소와 교환한다.
그 다음 최소힙의 성질을 만족하도록 해당 노드를 자식 노드와 교환한다.
자식 노드와 교환할 때 왼쪽과 오른쪽 자식 중 누구와 교환해야 할까?
- 최소힙의 속성을 유지하기 위해 더 작은 원소와 교환해 나간다.

트라이(접두사 트리)
트라이는 n-차 트리의 변형으로 각 노드에 문자를 저장하는 자료구조이다.
트리를 아래쪽으로 순회하면 단어 하나가 나오게 된다.
널 노드(null node) 혹은 ‘ * 노드 ‘ 는 종종 단어의 끝을 나타내주기 위해 사용된다.
트라이에서 각 노드는 1개에서 <알파벳_사이즈 + 1> 개까지 자식을 갖고 있을 수 있다.
트라이를 통해 유효한 단어의 접두사를 빠르게 확인할 수 있으며 이는 길이가 K인 문자열이 주어졌을 때 O(K) 시간이 소요된다.
참고