2020-04-10

Python / Pytorch

6 minutes read (About 961 words)

Pytorch_Multi_Layer_Perceptron_MLP

Pytorch Multi Layer Perceptron(MLP)에 관하여 with code

모두를 위한 딥러닝 - 파이토치 강의 참고

perceptron은 입력값 x에 대해 weight를 곱하고 bias를 더한 후 activation function을 거쳐서 나온 output을 통해 두가지의 class를 가지는 AND, OR 문제를 해결하기 위해 고안되었습니다.
AND gate는 다음과 같이 표로 나타낼 수 있습니다.

A	B	Output
0	0	0
0	1	0
1	0	0
1	1	1

위의 표는 매우 익숙하지만 이를 그래프로 나타내면 다음과 같이도 나타낼 수 있습니다.
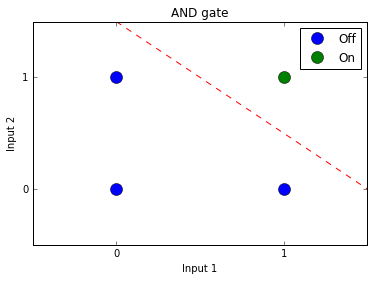
위의 그래프에서 0과 1을(off와 on)을 선 하나를 통해서 구분할 수 있는 방법은 빨간 점선으로 표시되어 있습니다. 즉, 하나의 선으로 두 가지의 class를 구분할 수 있습니다.
OR gate도 마찬가지 입니다.

A	B	Output
0	0	0
0	1	1
1	0	1
1	1	1

위와 같은 OR gate표를 그래프로 나타내면 다음과 같습니다.
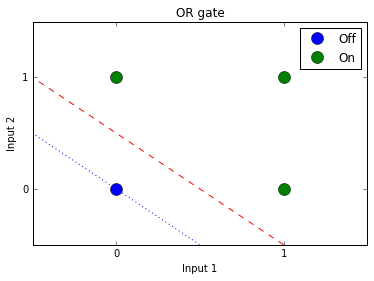
OR gate 그래프에서도 0과 1(off와 on)을 하나의 선으로 구분할 수 있습니다. 즉, AND gate와 마찬가지로 하나의 선으로 두 가지의 class를 구분할 수 있다는 뜻입니다.
다시 말해, AND 와 OR gate는 하나의 Layer를 가지는 perceptron으로 구분이 가능했습니다.
하지만, XOR gate는 달랐습니다.
XOR gate를 표로 나타내면 다음과 같습니다.

A	B	Output
0	0	0
0	1	1
1	0	1
1	1	0

이와같이 입력이 같으면 0을 다르면 1을 되돌려주는 XOR gate를 그래프로 나타내면 다음과 같습니다.
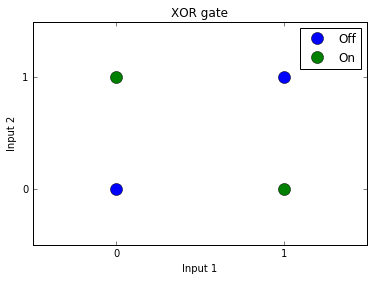
위와 같은 그래프에서 0과 1(off와 on)을 하나의 선으로 구분할 수 없었습니다. 즉, 하나의 perceptron으로는 AND/OR gate 문제는 해결할 수 있었지만 XOR gate 문제를 해결할 수 없었습니다.
이렇게 하나의 perceptron으로 해결할 수 없는 문제를 해결하기 위해 등장한것이 Multi Layer Perceptron입니다.
다시 한번 위의 그래프를 봤을때, 하나의 선이 아니라 두개의 선으로는 0과 1(off와 on)을 구분할 수 있을까요?
답은 YES입니다. 즉, 두개 이상의 perceptron으로는 XOR gate문제를 해결할 수 있었습니다.
4개의 Layer를 갖는 모델을 구현해 확인해 보겠습니다.
먼저 XOR gate에 해당하는 데이터를 만들고,

1
2
3

# XOR 데이터
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]]).to(device)
Y = torch.FloatTensor([[0], [1], [1], [0]]).to(device)

4개의 layer를 생성해 모델을 정의해줍니다.

# 4개의 레이어가 있는 MLP(Multi Layer Perceptron)
linear1 = torch.nn.Linear(2, 10, bias=True)
linear2 = torch.nn.Linear(10, 10, bias=True)
linear3 = torch.nn.Linear(10, 10, bias=True)
linear4 = torch.nn.Linear(10, 1, bias=True)
sigmoid = torch.nn.Sigmoid()

# 모델 정의
model = torch.nn.Sequential(linear1, sigmoid, linear2, sigmoid, linear3, sigmoid,
                            linear4, sigmoid).to(device)

이후 loss와 optimizer를 정의해주고,

1
2
3

#  loss / optimizer 정의
criterion = torch.nn.BCELoss().to(device)
optimizer = torch.optim.SGD(model.parameters(), lr=1)

모델을 통해 weight와 bias를 학습합니다.

# 학습
for epoch in range(10001):
    optimizer.zero_grad()
    hypothesis = model(X)

    loss = criterion(hypothesis, Y)
    loss.backward()
    optimizer.step()

    if epoch % 100 == 0:
        print(epoch, loss.item())
#>>> print
0 0.6948983669281006
100 0.6931558847427368
200 0.6931535005569458
.
.
.
9800 0.00016415018762927502
9900 0.00016021561168599874
10000 0.0001565046259202063

학습이 끝나면 실제값과 예측값이 잘 맞아 떨어지는지 확인합니다.

# 학습 후 실제값과 예측값 비교해보기
with torch.no_grad():
    hypothesis = model(X)
    predict = (hypothesis > 0.5).float()
    accuracy = (predict == Y).float().mean()

    print('Hyptthesis : ', hypothesis.detach().cpu().numpy(),
          '\nCorrect : ',predict.detach().cpu().numpy(),
          '\nAccuracy : ',accuracy.item())
#>>> print
Hyptthesis :  [[1.1168354e-04]
 [9.9982882e-01]
 [9.9984241e-01]
 [1.8533420e-04]] 
Correct :  [[0.]
 [1.]
 [1.]
 [0.]] 
Accuracy :  1.0

위의 결과를 통해 Multi Layer Perceptron을 사용하면 XOR gate문제를 해결할 수 있음을 확인했습니다.
참고

Full Code

# Python, Pytorch

Pytorch_Multi_Layer_Perceptron_MLP

Pytorch Multi Layer Perceptron(MLP)에 관하여 with code

모두를 위한 딥러닝 - 파이토치 강의 참고

Full Code

Like this article? Support the author with

Comments

Links

Categories

Tag Cloud

Recent

Archives

Tags

Recent

Archives

Tags

Your browser is out-of-date!